Posts Tagged: arithmetic
mental and environmental arithmetic
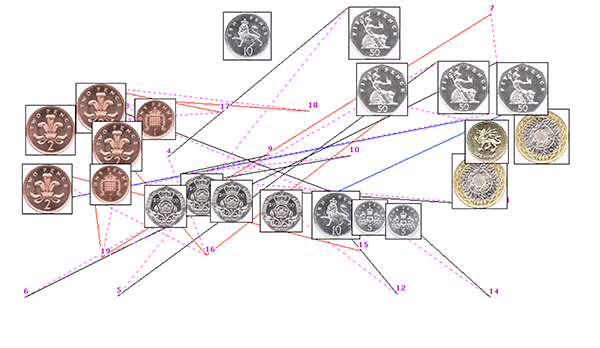
Paper: Interactive coin addition
| ‘Can you do Addition?’ the White Queen asked. ‘What’s one and one and one and one and one and one and one and one and one and one?’ ‘I don’t know,’ said Alice. ‘I lost count.’ |
| Lewis Carroll, Through the Looking-Glass, Chapter IX. |
Hansjörg Neth, Stephen J. Payne
Interactive coin addition: How hands can help us think
Abstract: Does using our hands help us to add the value of a set of coins?

Chapter: The cognitive basis of arithmetic
| The truths about numbers are in us; but still we learn them. |
| G.W. Leibniz (1765), Nouveaux essais sur l’entendement humain, p. 85 |
Helen De Cruz, Hansjörg Neth, Dirk Schlimm
The cognitive basis of arithmetic
Overview: Arithmetic is the theory of the natural numbers and one of the oldest areas of mathematics. Since almost all other mathematical theories make use of numbers in some way or other, arithmetic is also one of the most fundamental theories of mathematics. But numbers are not just abstract entities that are subject to mathematical ruminations — they are represented, used, embodied, and manipulated in order to achieve many different goals, e.g., to count or denote the size of a collection of objects, to trade goods, to balance bank accounts, or to play the lottery. Consequently, numbers are both abstract and intimately connected to language and to our interactions with the world. In the present paper we provide an overview of research that has addressed the question of how animals and humans learn, represent, and process numbers.
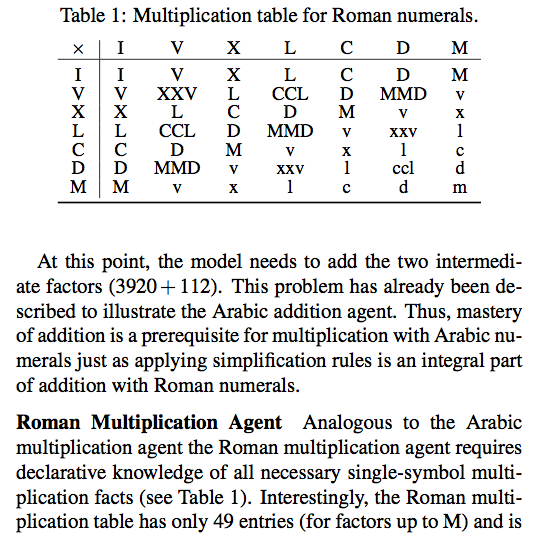

Paper: Arithmetic with Arabic vs. Roman numerals
| … how information is represented can greatly affect how easy it is to do different things with it. (…) it is easy to add, to subtract, and even to multiply if the Arabic or binary representations are used, but it is not at all easy to do these things — especially multiplication — with Roman numerals. This is a key reason why the Roman culture failed to develop mathematics in the way the earlier Arabic cultures had. |
| D Marr (1982): Vision, p. 21 |
Dirk Schlimm, Hansjörg Neth
Modeling ancient and modern arithmetic practices: Addition and multiplication with Arabic and Roman numerals
Abstract: To analyze the task of mental arithmetic with external representations in different number systems we model algorithms for addition and multiplication with Arabic and Roman numerals. This demonstrates that Roman numerals are not only informationally equivalent to Arabic ones but also computationally similar — a claim that is widely disputed. An analysis of our models’ elementary processing steps reveals intricate trade-offs between problem representation, algorithm, and interactive resources. Our simulations allow for a more nuanced view of the received wisdom on Roman numerals. While symbolic computation with Roman numerals requires fewer internal resources than with Arabic ones, the large number of needed symbols inflates the number of external processing steps.


Paper: Addition as interactive problem solving
| These dual skills of manipulating the environment and processing the environment (…) allow us to reduce very complex problems to a series of very simple ones. (…) This is real symbol processing and, we are beginning to think, the primary symbol processing that we are able to do. Indeed, on this view, the external environment becomes a key extension to our mind. |
| McClelland, Rumelhart and the PDP Research Group (1986): Vol. 2, p. 46 |
Hansjörg Neth, Stephen J. Payne
Addition as interactive problem solving
Abstract: Successful problem solving depends on a dynamic interplay of resources between agent, task, and task environment. To illuminate these interactions we studied how participants added a series of single-digit numbers presented on a computer screen. We distinguished between four different user interfaces, each implementing a different mode of interaction with the displayed addends: look only, point, mark, and move. By collecting and analysing complete interaction protocols we were able to integrate overall performance measures with fine-grained behavioural process data on the strategies engendered by the different user interfaces. We discovered reliable differences in the chosen sequences of addends, which can be understood in terms of the cost-benefit structures provided by the interactive resources of the user interfaces.
Keywords: Embodied cognition, mental arithmetic, epistemic actions, complementary strategies, immediate interactive behavior (IIB).
Reference: Neth, H., & Payne, S. J. (2001). Addition as interactive problem solving. In J. D. Moore & K. Stenning (Eds.), Proceedings of the 23rd Annual Meeting of the Cognitive Science Society (pp. 698–703). Mahwah, NJ: Lawrence Erlbaum.
Related: Thinking by doing? | Immediate interactive behavior (IIB) | Arabic vs. Roman arithmetic | Taxonomy of actions | The cognitive basis of arithmetic | Interactive coin addition | The functional task environment
Resources: Download PDF | Google Scholar