Posts in Category: problem solving
problem solving
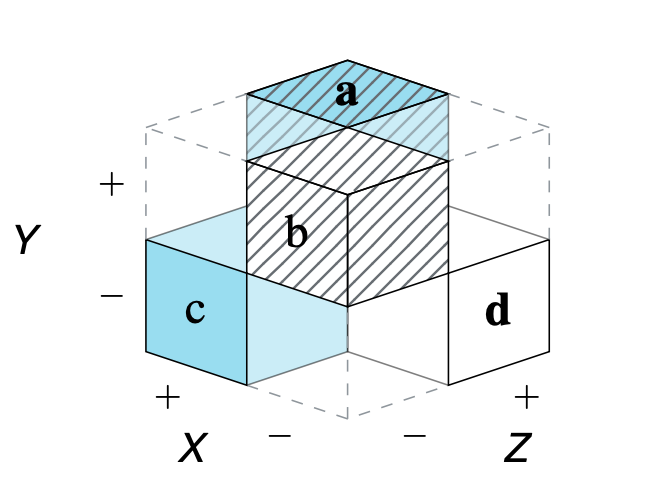
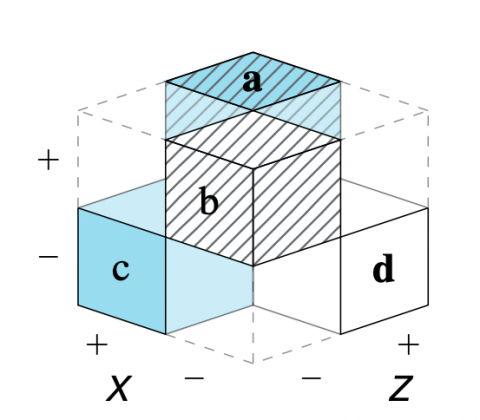
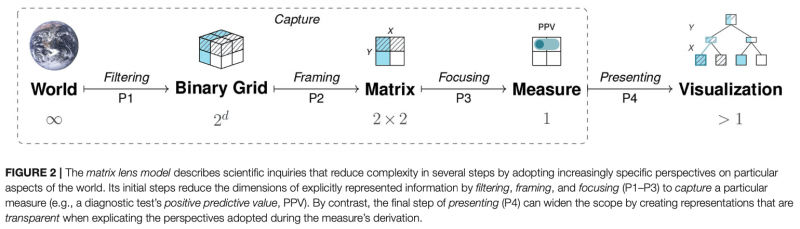
Paper: Perspectives on the 2×2 Matrix
Hansjörg Neth, Nico Gradwohl, Dirk Streeb, Daniel A. Keim, Wolfgang Gaissmaier
Perspectives on the 2×2 matrix: Solving semantically distinct problems based on a shared structure of binary contingencies
Abstract
Cognition is both empowered and limited by representations. The matrix lens model explicates tasks that are based on frequency counts, conditional probabilities, and binary contingencies in a general fashion. Based on a structural analysis of such perspective on representational accounts of cognition that recognizes representational isomorphs as opportunities, rather than as problems.
The shared structural construct of a 2×2 matrix supports a set of generic tasks and semantic mappings that provide a tasks, the model links several problems and semantic domains and provides a new unifying framework for understanding problems and defining scientific measures. Our model’s key explanatory mechanism is the adoption of particular perspectives on a 2×2 matrix that categorizes the frequency counts of cases by some condition, treatment, risk, or outcome factor. By the selective steps of filtering, framing, and focusing on specific aspects, the measures used in various semantic domains negotiate distinct trade-offs between abstraction and specialization. As a consequence, the transparent communication of such measures must explicate the perspectives encapsulated in their derivation.
To demonstrate the explanatory scope of our model, we use it to clarify theoretical debates on biases and facilitation effects in Bayesian reasoning and to integrate the scientific measures from various semantic domains within a unifying framework. A better understanding of problem structures, representational transparency, and the role of perspectives in the scientific process yields both theoretical insights and practical applications.
Why read this paper?
This paper is quite long and covers a wide array of concepts and topics. So what can you expect to gain from reading it?
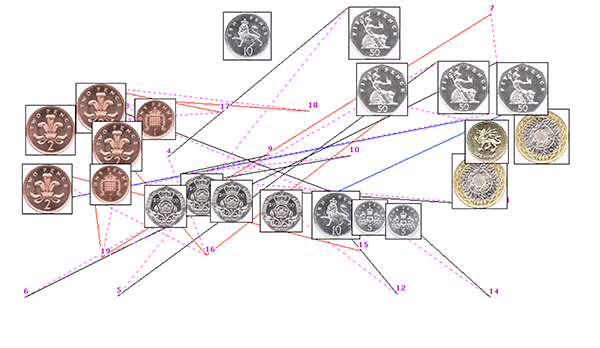
Paper: Interactive coin addition
| ‘Can you do Addition?’ the White Queen asked. ‘What’s one and one and one and one and one and one and one and one and one and one?’ ‘I don’t know,’ said Alice. ‘I lost count.’ |
| Lewis Carroll, Through the Looking-Glass, Chapter IX. |
Hansjörg Neth, Stephen J. Payne
Interactive coin addition: How hands can help us think
Abstract: Does using our hands help us to add the value of a set of coins?


Paper: A taxonomy of (practical vs. theoretical) actions
| The solution to a problem changes the problem. |
| Peer’s Law |
Hansjörg Neth, Thomas Müller
Thinking by doing and doing by thinking: A taxonomy of actions
Abstract: Taking a lead from existing typologies of actions in the philosophical and cognitive science literatures, we present a novel taxonomy of actions.
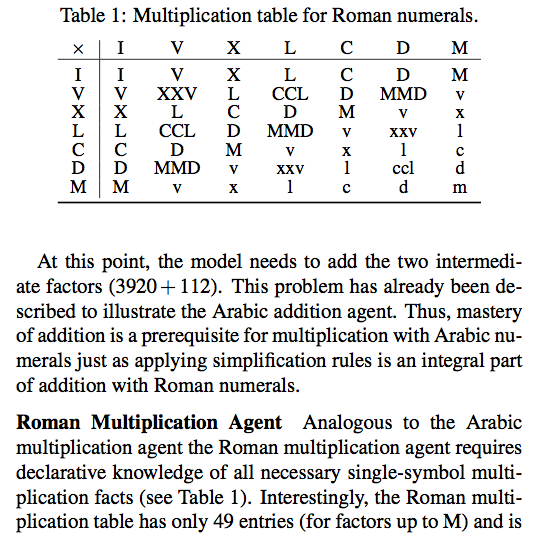

Paper: Arithmetic with Arabic vs. Roman numerals
| … how information is represented can greatly affect how easy it is to do different things with it. (…) it is easy to add, to subtract, and even to multiply if the Arabic or binary representations are used, but it is not at all easy to do these things — especially multiplication — with Roman numerals. This is a key reason why the Roman culture failed to develop mathematics in the way the earlier Arabic cultures had. |
| D Marr (1982): Vision, p. 21 |
Dirk Schlimm, Hansjörg Neth
Modeling ancient and modern arithmetic practices: Addition and multiplication with Arabic and Roman numerals
Abstract: To analyze the task of mental arithmetic with external representations in different number systems we model algorithms for addition and multiplication with Arabic and Roman numerals. This demonstrates that Roman numerals are not only informationally equivalent to Arabic ones but also computationally similar — a claim that is widely disputed. An analysis of our models’ elementary processing steps reveals intricate trade-offs between problem representation, algorithm, and interactive resources. Our simulations allow for a more nuanced view of the received wisdom on Roman numerals. While symbolic computation with Roman numerals requires fewer internal resources than with Arabic ones, the large number of needed symbols inflates the number of external processing steps.