Posts in Category: chapter
book chapter or chapter in collection


Article: Heuristics — Tools for an uncertain world
to treat everything as if it were a nail.
Abraham H. Maslow (1966, p. 15f.)
Hansjörg Neth, Gerd Gigerenzer
Heuristics: Tools for an uncertain world
We distinguish between situations of risk, where all options, consequences, and probabilities are known, and situations of uncertainty, where they are not. Probability theory and statistics are the best tools for deciding under risk but not under uncertainty, which characterizes most relevant problems that humans have to solve. Uncertainty requires simple heuristics that are robust rather than optimal.


Kapitel: Das Potenzial einfacher Heuristiken in Controlling und Management Reporting
Hansjörg Neth
Wenn weniger mehr ist: Das Potenzial einfacher Heuristiken in Controlling und Management Reporting
Zusammenfassung:
- Controller sammeln Daten, berechnen präzise Kennzahlen und bereiten in Berichten möglichst viele Informationen sehr gewissenhaft auf – und verfehlen ihren Auftrag vielleicht gerade dadurch. Der Versuch, stets alle verfügbaren Daten zu berücksichtigen und in Entscheidungen einfliessen zu lassen, entspricht dem klassischen Ideal des Homo oeconomicus.
- Diese gründliche Vorgehensweise wurde für eine Welt des Risikos entwickelt, wird aber unkritisch auf Entscheidungen unter Unsicherheit übertragen. Zudem eignet sie sich eher zur Erklärung der Vergangenheit, soll in der Praxis aber Vorhersagen für die Zukunft liefern.
- Homo heuristicus stellt einen modernen Gegenentwurf zum Homo oeconomicus dar. Er nutzt einfache Heuristiken, die Informationen selektieren und ignorieren um robuste Vorhersagen unter Unsicherheit zu ermöglichen.
- Ein guter Bericht muss Prozesse transparent machen und nützliche Kennzahlen sollten den Weg weisen, anstatt nur Ergebnisvariablen abzubilden. Statt defensivem Entscheiden brauchen Unternehmen eine Fehlerkultur, in der man aus Fehlern lernen kann.
- Die Analyse von Heuristiken zeigt, wann und warum man sich auf seine Instinkte und Intuitionen verlassen kann und soll. In allen Bereichen, in denen Erfahrung eine Rolle spielt, wäre es unklug und fahrlässig, das Bauchgefühl von Experten geringer einzuschätzen als betriebliche Kennzahlen und statistische Zahlenkolonnen.

Chapter: The cognitive basis of arithmetic
| The truths about numbers are in us; but still we learn them. |
| G.W. Leibniz (1765), Nouveaux essais sur l’entendement humain, p. 85 |
Helen De Cruz, Hansjörg Neth, Dirk Schlimm
The cognitive basis of arithmetic
Overview: Arithmetic is the theory of the natural numbers and one of the oldest areas of mathematics. Since almost all other mathematical theories make use of numbers in some way or other, arithmetic is also one of the most fundamental theories of mathematics. But numbers are not just abstract entities that are subject to mathematical ruminations — they are represented, used, embodied, and manipulated in order to achieve many different goals, e.g., to count or denote the size of a collection of objects, to trade goods, to balance bank accounts, or to play the lottery. Consequently, numbers are both abstract and intimately connected to language and to our interactions with the world. In the present paper we provide an overview of research that has addressed the question of how animals and humans learn, represent, and process numbers.
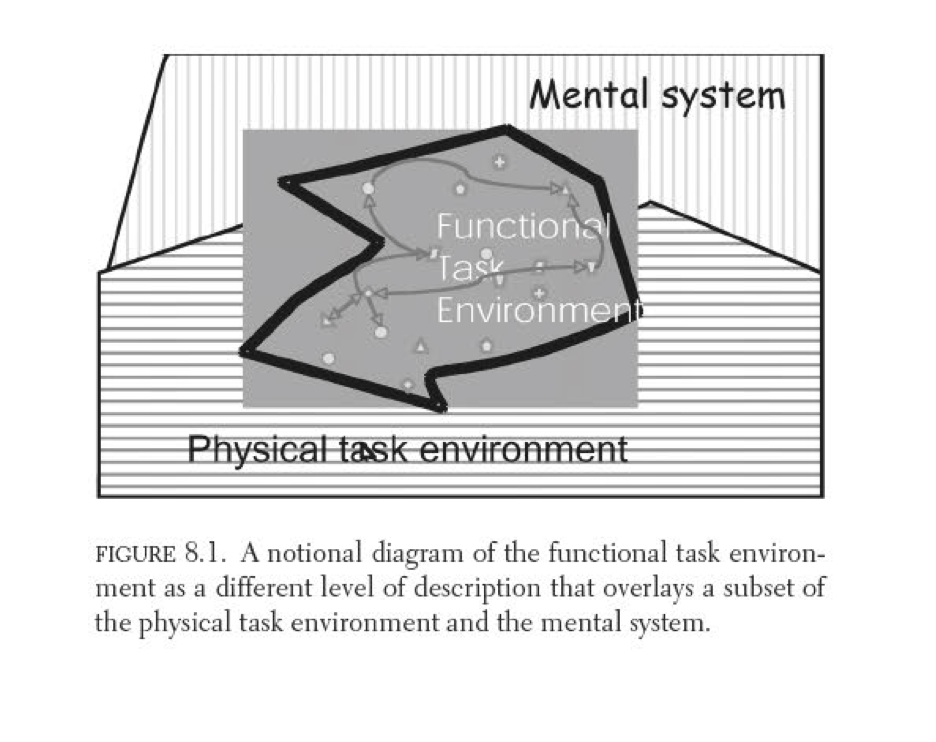
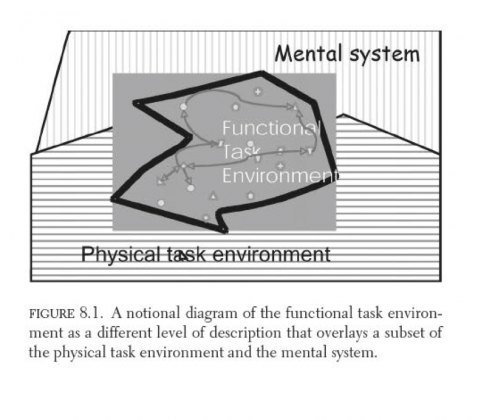
Chapter: The functional task environment
The apparent complexity of our behavior over time is largely a reflection
of the complexity of the environment in which we find ourselves.
(Simon, 1996, p. 53)
Wayne D. Gray, Hansjörg Neth, Michael J. Schoelles
The functional task environment
From the introduction: Although human thought may be possible in those floatation tanks that are used to encourage meditative states, in by far the majority of instances thought occurs in the context of some physical task environment. The physical environment can be as simple as a light and book. It can be as complex as the face of a mountain and the equipment of the climber. It may be as dynamic as the cockpit of an F-16 in supersonic flight and as reactive as a firefight in Iraq or as heated as an argument between lovers.