Posts Tagged: PhD
Ph.D.-related posts and papers


Paper: Decade effects in mental addition
| The most important part of the Analytical Engine was undoubtedly the mechanical method of carrying the tens. (…) The difficulty did not consist so much in the more or less complexity of the contrivance as in the reduction of the time required to effect the carriage. (…) nothing but teaching the Engine to foresee and then to act upon that foresight could ever lead me to the object I desired… |
| Charles S. Babbage (1864), Passages from the Life of a Philosopher, p. 114 |
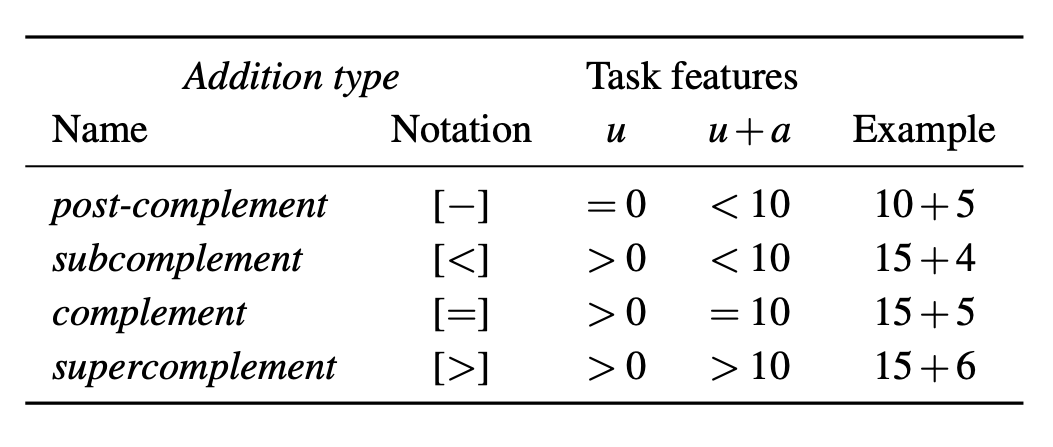
Classification of addition types for adding a single-digit addend a (with a∈{1…9}) to an augend Au (u denoting the augend’s unit). (See Table 1 for details.)
Hansjörg Neth, Stephen J. Payne
Decade effects in mental addition
We examine representational effects of Western numerals on mental arithmetic. An analysis of mental addition tasks using a base-10 place-value notation yields a taxonomy of addition types that is anchored in the notion of complements (i.e. additions with round sums). Two experimental studies use a paradigm of serial addition that presents lists of numbers to adult participants, who mentally represent all intermediate steps. In study 1, participants add sequences of single-digit addends in a self-paced fashion. Study 2 extends this paradigm by simultaneously presenting two addends, thus allowing for a modicum of strategic choice. Both studies vary the number of complements within the lists and measure addition accuracy and latency. Beyond decade and carry effects, our results show that lists containing or enabling complements are easier to add. Addition latencies jointly depend on addition type and problem size. When adders have some discretion about the order of choosing addends, they adaptively exploit the difficulty of addition types by tailoring their sequences to decade boundaries. One motivation for seeking complements lies in enabling subsequent post-complements. Reflecting on the dynamic interplay between numeric representations, strategic choices and cognitive adaptations, we discuss implications for psychological explanations, technology and design.
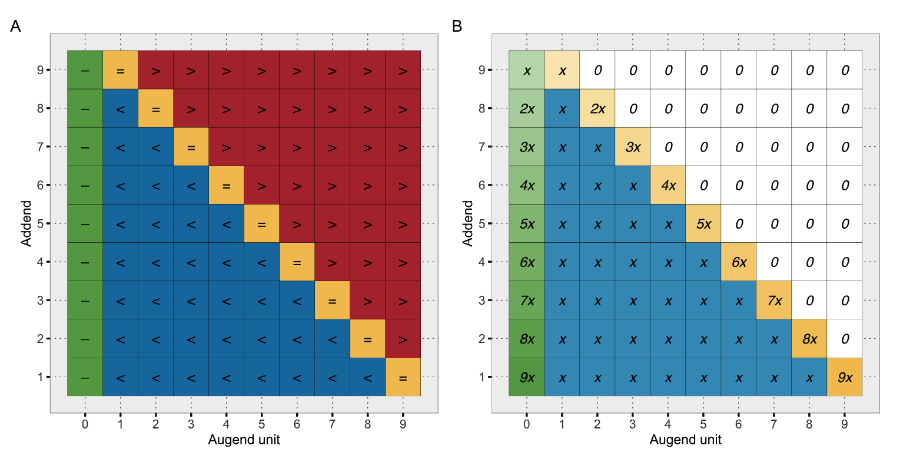
Four different addition types (A) and their hypothetical frequency (B, assuming uniform distribution of addends 1–9 and full decomposition of super-complements). (See Figure 4 in Appendix A1 for details.)
This article is part of the theme issue A solid base for scaling up: the structure of numeration systems.
Keywords: mental arithmetic, addition strategies, base notation, representational effects.
Reference: Neth, H., & Payne, S. J. (2025). Decade effects in mental addition. Philosophical Transactions of the Royal Society B, 380, 20240220. https://doi.org/10.1098/rstb.2024.0220
Related: Addition as interactive problem solving | Thinking by doing? | Immediate interactive behavior (IIB) | Arabic vs. Roman arithmetic | Taxonomy of actions | The cognitive basis of arithmetic | Interactive coin addition | The functional task environment
Resources: open access article | PDF download | Google Scholar
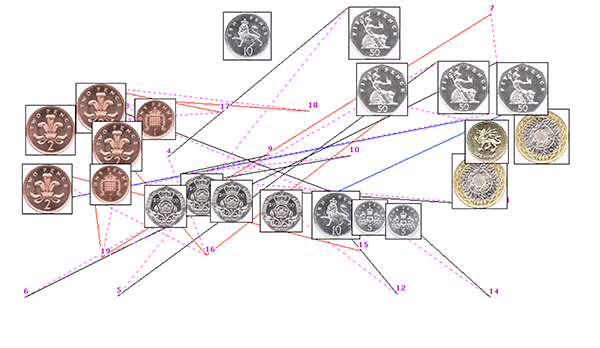
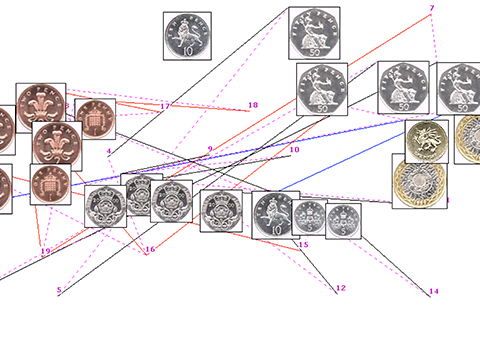
Paper: Interactive coin addition
| ‘Can you do Addition?’ the White Queen asked. ‘What’s one and one and one and one and one and one and one and one and one and one?’ ‘I don’t know,’ said Alice. ‘I lost count.’ |
| Lewis Carroll, Through the Looking-Glass, Chapter IX. |
Hansjörg Neth, Stephen J. Payne
Interactive coin addition: How hands can help us think
Abstract: Does using our hands help us to add the value of a set of coins?


Paper: A taxonomy of (practical vs. theoretical) actions
| The solution to a problem changes the problem. |
| Peer’s Law |
Hansjörg Neth, Thomas Müller
Thinking by doing and doing by thinking: A taxonomy of actions
Abstract: Taking a lead from existing typologies of actions in the philosophical and cognitive science literatures, we present a novel taxonomy of actions.
Paper: Immediate interactive behavior (IIB)
| … immediate behavior, responses that must be made to some stimulus within very approximately one second (that is, roughly from ~300 ms to ~3 sec). (…) … immediate behavior is where the architecture shows through — where you can see the cognitive wheels turn and hear the cognitive gears grind. Immediate behavior is the appropriate arena in which to discover the nature of the cognitive architecture. |
| A. Newell (1990), Unified theories of cognition, p. 235f. |
Hansjörg Neth, Richard A. Carlson, Wayne D. Gray, Alex Kirlik, David Kirsh, Stephen J. Payne
Immediate interactive behavior: How embodied and embedded cognition uses and changes the world to achieve its goals
Summary: We rarely solve problems in our head alone. Instead, most real-world problem solving and routine behavior recruits external resources and achieves its goals through an intricate process of interaction with the physical environment. Immediate interactive behavior (IIB) entails all adaptive activities of agents that routinely and dynamically use their embodied and environmentally embedded nature to augment cognitive processes. IIB also characterizes an emerging domain of cognitive science research that studies how cognitive agents exploit and alter their task-environments in real-time. Examples of IIB include arranging coins when adding their values, solving a problem with paper and pencil, arranging tools and ingredients while preparing a meal, programming a VCR, and flying an airplane.