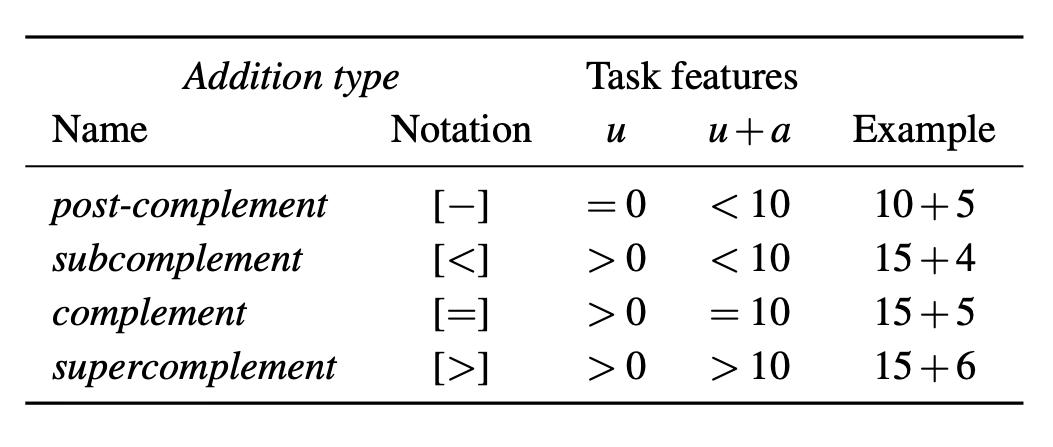
Classification of addition types for adding a single-digit addend a (with a∈{1…9}) to an augend Au (u denoting the augend’s unit). (See Table 1 for details.)

Hansjörg Neth, Stephen J. Payne

Decade effects in mental addition 

We examine representational effects of Western numerals on mental arithmetic. An analysis of mental addition tasks using a base-10 place-value notation yields a taxonomy of addition types that is anchored in the notion of complements (i.e. additions with round sums). Two experimental studies use a paradigm of serial addition that presents lists of numbers to adult participants, who mentally represent all intermediate steps.  In study 1, participants add sequences of single-digit addends in a self-paced fashion.  Study 2 extends this paradigm by simultaneously presenting two addends, thus allowing for a modicum of strategic choice. Both studies vary the number of complements within the lists and measure addition accuracy and latency.  Beyond decade and carry effects, our results show that lists containing or enabling complements are easier to add. Addition latencies jointly depend on addition type and problem size. When adders have some discretion about the order of choosing addends, they adaptively exploit the difficulty of addition types by tailoring their sequences to decade boundaries. One motivation for seeking complements lies in enabling subsequent post-complements. Reflecting on the dynamic interplay between numeric representations, strategic choices and cognitive adaptations, we discuss implications for psychological explanations, technology and design.

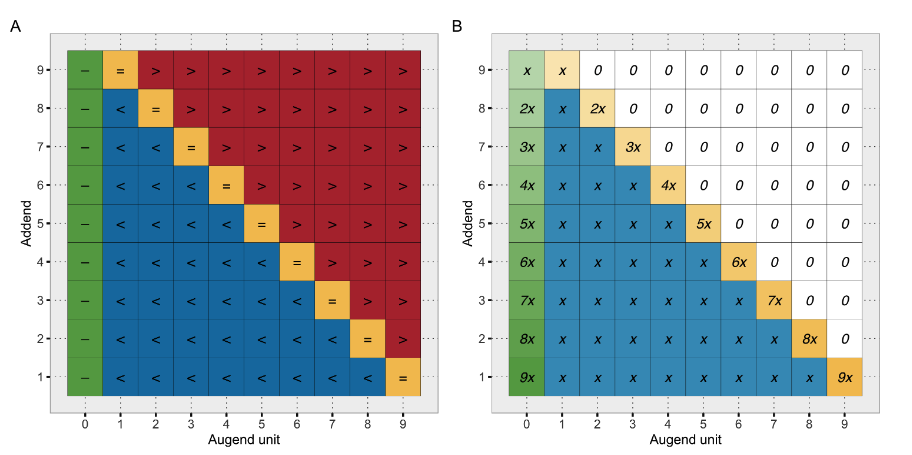
Four different addition types (A) and their hypothetical frequency (B, assuming uniform distribution of addends 1–9 and full decomposition of super-complements). (See Figure 4 in Appendix A1 for details.)

This article is part of the theme issue A solid base for scaling up: the structure of numeration systems.

Keywords:  mental arithmetic, addition strategies, base notation, representational effects.

Reference:  Neth, H., & Payne, S. J. (2025).  Decade effects in mental addition. Philosophical Transactions of the Royal Society B, 380, 20240220.  https://doi.org/10.1098/rstb.2024.0220 

Related:  Addition as interactive problem solving | Thinking by doing? | Immediate interactive behavior (IIB) | Arabic vs. Roman arithmetic | Taxonomy of actions | The cognitive basis of arithmetic | Interactive coin addition | The functional task environment

Resources:  open access article | PDF download | Google Scholar