Posts Tagged: representation
representational issues, framing
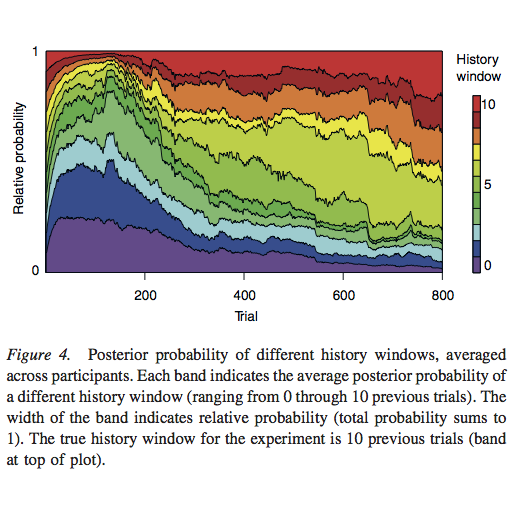
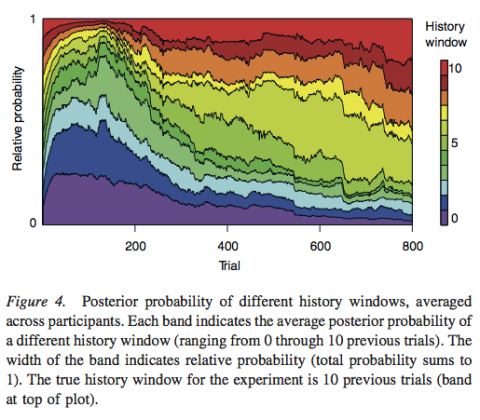
Paper: Melioration as rational choice
Melioration (…) is the dynamic process controlling allocation of time across response alternatives.
Herrnstein & Vaughan (1980). Melioration and behavioral allocation, p. 143+172
Chris R. Sims, Hansjörg Neth, Robert A. Jacobs, Wayne D. Gray
Melioration as rational choice: Sequential decision making in uncertain environments
Abstract: Melioration — defined as choosing a lesser, local gain over a greater longer term gain — is a behavioral tendency that people and pigeons share. As such, the empirical occurrence of meliorating behavior has frequently been interpreted as evidence that the mechanisms of human choice violate the norms of economic rationality. In some environments, the relationship between actions and outcomes is known. In this case, the rationality of choice behavior can be evaluated in terms of how successfully it maximizes utility given knowledge of the environmental contingencies. In most complex environments, however, the relationship between actions and future outcomes is uncertain and must be learned from experience. When the difficulty of this learning challenge is taken into account, it is not evident that melioration represents suboptimal choice behavior.


Paper: Ranking LOD data with a cognitive heuristic
Arjon Buikstra, Hansjörg Neth, Lael J. Schooler, Annette ten Teije, Frank van Harmelen
Ranking query results from Linked Open Data using a simple cognitive heuristic
Abstract: We address the problem how to select the correct answers to a query from among the partially incorrect answer sets that result from querying the Web of Data.

Chapter: The cognitive basis of arithmetic
| The truths about numbers are in us; but still we learn them. |
| G.W. Leibniz (1765), Nouveaux essais sur l’entendement humain, p. 85 |
Helen De Cruz, Hansjörg Neth, Dirk Schlimm
The cognitive basis of arithmetic
Overview: Arithmetic is the theory of the natural numbers and one of the oldest areas of mathematics. Since almost all other mathematical theories make use of numbers in some way or other, arithmetic is also one of the most fundamental theories of mathematics. But numbers are not just abstract entities that are subject to mathematical ruminations — they are represented, used, embodied, and manipulated in order to achieve many different goals, e.g., to count or denote the size of a collection of objects, to trade goods, to balance bank accounts, or to play the lottery. Consequently, numbers are both abstract and intimately connected to language and to our interactions with the world. In the present paper we provide an overview of research that has addressed the question of how animals and humans learn, represent, and process numbers.

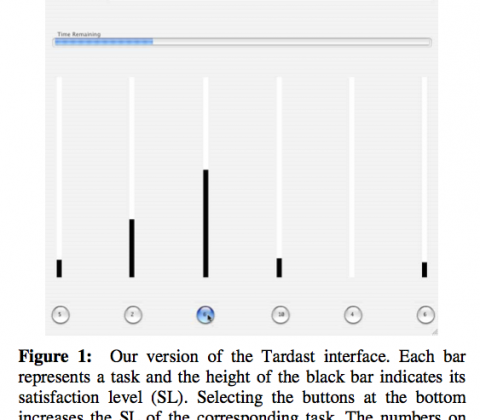
Paper: Feedback design for controlling a dynamic multitasking system
| If an organism is confronted with the problem of behaving approximately rationally, or adaptively, in a particular environment, the kinds of simplifications that are suitable may depend not only on the characteristics—sensory, neural, and other—of the organism, but equally on the nature of the environment. |
| H.A. Simon (1956), Rational choice and the structure of the environment, p. 130 |
Hansjörg Neth, Sangeet S. Khemlani, Wayne D. Gray
Feedback design for the control of a dynamic multitasking system: Dissociating outcome feedback from control feedback
Objective: We distinguish outcome feedback from control feedback to show that suboptimal performance in a dynamic multitasking system may be caused by limits inherent to the information provided rather than human resource limits.